Kelas :VII E & VII F
Hari/tgl : Kamis, 03 Oktober 2019
Operasi bentuk aljabar.
1. Operasi penjumlahan dan pengurangan
Operasi penjumlahan dan pengurangan bentuk aljabar hanya dapat dilakukan pada suku yang sejenis, dengan cara mengoperasikannya pada konstantanya.
contoh :

 -> tidak dapat dijumlahkan karena bukan suku yang sejenis
-> tidak dapat dijumlahkan karena bukan suku yang sejenis
 bisa dituliskan sebagai x saja.
bisa dituliskan sebagai x saja.
 -> bukan suku sejenis
-> bukan suku sejenis

2. Operasi perkalian
Ingat kembali bahwa pada operasi perkalian bilangan bulat terdapat sifat distributif pada penjumlahan dan pengurangan, yaitu a(b + c)= ab + ac , dan a(b – c) = ab – ac. Pada operasi perkalian bentuk aljabar sifat tersebut juga berlaku.
– Perkalian antara konstanta dengan bentuk aljabar.
Untuk melakukan operasi perkalian antara konstanta dengan bentuk aljabar, dapat dilakukan dengan mudah, yaitu dengan mengalikan konstanta tersebut dengan konstanta pada bentuk aljabar.
Contoh :




– perkalian antara dua bentuk aljabar.
Seperti pada perkalian antara konstanta dengan bentuk aljabar, dalam perkalian dua bentuk aljabar berlaku juga sifat distributif. Untuk suku yang sejenis, jika variabel dikalikan maka akan menjadi pangkat, misal  , sedangkan konstanta dikalikan seperti biasa. Untuk suku yang tidak sejenis maka variabelnya akan dituliskan saja, dan konstanta dikalikan seperti biasa.
, sedangkan konstanta dikalikan seperti biasa. Untuk suku yang tidak sejenis maka variabelnya akan dituliskan saja, dan konstanta dikalikan seperti biasa.
Perkalian satu suku dengan dua suku,

Perkalian antara dua suku,

Perkalian antara dua suku dengan tiga suku,

Contoh :


4. Operasi pembagian
Operasi pembagian pada bentuk aljabar dilakukan dengan cara membagi konstantanya seperti biasa, namun untuk variabelnya, dilihat dulu koefisien dari kedua variabel nya, kemudian bagi masing-masing variabelnya dengan koefisiennya.
Contoh :











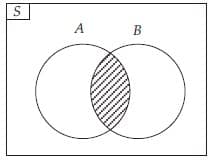 daerah irisan A dan B
daerah irisan A dan B

 Bukan fungsi karena terdapat anggota di A yang tidak dihubungkan dengan anggota di BBukan fungsi karena terdapat anggota di A yang dihubungkan lebih dari satu dengan anggota di BMeupakan fungsi karena setiap anggota di A tapat dihubungkan dengan satu anggota di B
Bukan fungsi karena terdapat anggota di A yang tidak dihubungkan dengan anggota di BBukan fungsi karena terdapat anggota di A yang dihubungkan lebih dari satu dengan anggota di BMeupakan fungsi karena setiap anggota di A tapat dihubungkan dengan satu anggota di B



