Soal Pengayaan Kelas 7 (16 - 18 Des 2019)

Pilihlah jawaban yang tepat !

1.  Hasil dari [6 + (- 9 )] x 5 – 18 : (-3) = adalah....

     A.  – 21          B. – 9          C. 9              D. 21

2. Jika  n × (20 : - 5) = 120, maka nilai n =....

     A.  – 30        B. – 15         C. 15         D. 30

3. Suhu udara di suatu kota di Eropa ketika musim dingin adalah – 10^oC. Ketika musim semi, suhu udara meningkat hingga menjadi 18^oC. Berapa selisih udara di kota tersebut antara musim dingin dan musim semi?

   A. – 28^oC     B. – 8^oC       C. 8^oC      D. 28^oC

4. Suatu kompetisi mempunyai aturan sebagai berikut;  Jika menang mendapat nilai 3, jika kalah mendapat nilai –2 dan jika seri mendapat nilai 1. Regu  Tangkas bermain 15 kali dengan hasil 8 kali menang dan 3 kali seri. Nilai yang didapat regu Tangkas adalah …..

   A.  – 7            B. 11              C. 19              D. 27

5.Faktor Persekutuan Terbesar (FPB) dari 36, 48 dan 72 adalah....

  A.  10            B. 12             C. 14                D. 15

6.Ibu memberi uang sebesar Rp 100.000,00 kepada Arina. Setiap hari Arina membelanjakan uangnya sebesar Rp 8.000,00. Jika sekarang sisa uang yang dimiliki Arina adalah Rp 12.000,00, maka berapa hari Arina sudah membelanjakan uangnya?

   A. 9            B. 10            C. 11              D. 12           

7.Bilangan pecahan diantara  ⁵/₉ dan ⁷/₁₂  adalah ……

    A. ⁶/₁₀        B. ²¹/₃₆         C. ⁴⁰/₇₂          D. ⁴¹/₇₂

8. ¹³/₂₀   diubah menjadi pecahan desimal adalah....

   A 0,75          B. 0,65           C. 0,58          D. 0,52

9.Hasil dari 8 ¹/₃ : 2 ²/₉ – ³/₄ x ( -²/₁₅) adalah….

   A. 7 ⁷/₁₀       B. 6 ⁷/₂₀         C. 4 ¹³/₂₀       D. 3 ¹⁷/₂₀

10. Pak Ahmad memiliki tanah seluas 24 ha. tanah tersebut ditanami pohon mangga  ¹/₃ bagian, ditanami jeruk ¹/₄ bagian, dan ¹/₆ bagian untuk kolam ikan dan sisanya ingin ditanami berbagai tanaman obat. Berapa luas tanah yang akan ditanami tanaman obat?

   A. 6 ha          B. 7,2 ha        C. 8 ha           D. 9 ha

11. Koefisien dari 5x² – 2x + 7 adalah....

   A.  x², x dan 1                      C. 5, - 2 dan 7

   B.  5, - 2 dan x                     D. 5 dan – 2

12. Kelipatan persekutuan terkecil (KPK) dari  8a²b³ dan 12a⁴b² adalah....

   A.  24a²b²        B. 24a⁴b³         C. 24a⁶b5         D. 24a⁸b⁶

13. Hasil dari 4a – 2ab – (a – 5b) =….

   A. 4a – 7b                              C. 3a – 2ab – 5a

   B. 5a – 5b                              D. 3a – 2ab + 5b

14. Hasil dari 3 (x + 2y) – 2 (2x – 5y) = ….

    A. – x + 16y                          C. x – 16y

    B.  – 7x + 8y                         D. 7x + 8y

15.Dari pernyataan berikut, yang benar adalah....

   A.  a(b – c) = ac – bc             C. a ( b – c)  = ba – bc   

   B.  a (b – c) = cb – ca            D. a  (b – c) = ab – ac

16. Hasil dari (2x  + 3) (x – 5) adalah....

   A.  2x² – 7x – 15                   C. 2x² + 8x – 15

   B.  2x² + 7x – 15                   D. 2x² – 2x – 15

17. Hasil dari 12a²b³ : 4ab =....

   A.  3a³b²           B. 3ab²           C. 3a²b           D. 3a²b²

18. Diketahui X = {x | x ≤ 8, x є bilangan prima) dan Y = {x | - 2 ≤ x ≤ 5, x є bilangan bulat}, maka anggota (X ∩ Y) adalah ....
   A. {1, 2, 3, 5}                      C. {-1, 0, 1, 2, 3, 4}
   B. {2, 3,  5}                         D. {-1, 2, 3, 4, 5}

19. Diketahui : K = {x | -2 ≤ x ≤ 3; x є bilangan bulat} dan L = {x | 0 < x ≤ 5; x є bilangan ganjil}. Maka K – L adalah ....
   A. {-1, 0, 1, 2, 3}                 C. {-2, -1, 0, 2}
   B. {-1, 0, 1, 2}                     D. {2, 3, 5}

20. Diketahui B = {p,q,r,s}. Banyaknya himpunan bagian dari B adalah ....
   A. 4                B. 8               C. 16              D. 32

21. Jika n(S) = 155, n(P) = 100, n(Q) = 120 dan n (P ∩ Q)= 80, maka n(P ∪ Q)^c adalah....

   A. 15              B. 35              C. 55              D. 140

22. Dari 42 anak, terdapat 23  anak gemar makan permen dan 17 gemar makan coklat. Jika  9 anak tidak gemar makan permen dan coklat, maka banyaknya anak yang gemar makan coklat dan permen adalah .... anak.
   A. 5               B. 6                C. 7                D. 8

23. Suatu kelas  terdapat 30 anak. 15 anak suka menggambar, 20 anak suka menyanyi, dan 4 anak tidak suka kedua-duanya. Banyaknya anak yang  hanya suka menggambar adalah ....
   A. 6               B. 7                C. 8                D. 9

24. Pernyataan di bawah ini yang bukan persamaan linear satu variabel adalah....

   A. a + 2 = 6                          C. x – 21 = 8x                    

   B.  y + 8 = 4y – 6                   D. 3x – y = 10

SPLDV

Hari,tgl : Jumat, 29 Nopember 2019

Kelas : VIII A

METODE GABUNGAN UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR (SPLDV)

Dalam materi Sistem Persamaan Linear Dua Variabel, sebelumnya kita sudah pernah membahas dua metode yang bisa dipakai untuk menentukan himpunan penyelesaian SPLDV, yang akan dibahas kali ini yaitu metode gabungan. Metode gabungan adalah suatu metode yang digunakan untuk menentukan himpunan penyelesaian suatu SPLDV dengan cara menggunakan dua metode sekaligus yakni metode eliminasi dan metode substitusi.
Pertama bisa menggunakan metode eliminasi untuk mencari salah satu nilai variabel. Langkah berikutnya setelah nilai variabel didapatkan, maka nilai variabel tersebut kita substitusikan untuk mendapatkan variabel yang lain. Supaya lebih paham kita bahas bersama-sama contoh soal di bawah ini.

CONTOH 1

Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel x + 2y = 6 dan 2x – y = 6 dengan menggunakan metode gabungan!
x + 2y = 6………….(1)
2x – y = 6………….(2)
Langkah I eliminasi salah satu variabel
Pertama kita harus mengeliminasi variabel x

x + 2y = 6	x 2	2x + 4y = 12
2x – y = 6	x 1	2x – 2y =   6   –
		6y   = 6
		y = 1

Dari langkah I diperoleh y = 1
Selanjutnya untuk memperoleh nilai x, substitusikan nilai y = 1 ke persamaan (1)
yaitu x + 2y = 6
x + 2(1) = 6
=> x + 2 = 6
=> x = 6 – 2
=> x = 4
Jadi, himpunan penyelesaian dari SPLDVdari persamaan x + 2y = 6 dan 2x – y = 6
adalah {(4, 1)}.

Contoh Soal PAS Kelas 7

Hari/tgl : Kamis, 28 Nopember 2019

Kelas : VII E & VII F

Pilihlah jawaban yang tepat !

1.  Hasil dari [6 + (- 9 )] x 5 – 18 : (-3) = adalah....

     A.  – 21          B. – 9          C. 9              D. 21

2. Jika  n × (20 : - 5) = 120, maka nilai n =....

     A.  – 30        B. – 15         C. 15         D. 30

3. Suhu udara di suatu kota di Eropa ketika musim dingin adalah – 10^oC. Ketika musim semi, suhu udara meningkat hingga menjadi 18^oC. Berapa selisih udara di kota tersebut antara musim dingin dan musim semi?

   A. – 28^oC     B. – 8^oC       C. 8^oC      D. 28^oC

4. Suatu kompetisi mempunyai aturan sebagai berikut;  Jika menang mendapat nilai 3, jika kalah mendapat nilai –2 dan jika seri mendapat nilai 1. Regu  Tangkas bermain 15 kali dengan hasil 8 kali menang dan 3 kali seri. Nilai yang didapat regu Tangkas adalah …..

   A.  – 7            B. 11              C. 19              D. 27

5.Faktor Persekutuan Terbesar (FPB) dari 36, 48 dan 72 adalah....

  A.  10            B. 12             C. 14                D. 15

6.Ibu memberi uang sebesar Rp 100.000,00 kepada Arina. Setiap hari Arina membelanjakan uangnya sebesar Rp 8.000,00. Jika sekarang sisa uang yang dimiliki Arina adalah Rp 12.000,00, maka berapa hari Arina sudah membelanjakan uangnya?

   A. 9            B. 10            C. 11              D. 12           

7.Bilangan pecahan diantara  ⁵/₉ dan ⁷/₁₂  adalah ……

    A. ⁶/₁₀        B. ²¹/₃₆         C. ⁴⁰/₇₂          D. ⁴¹/₇₂

8. ¹³/₂₀   diubah menjadi pecahan desimal adalah....

   A 0,75          B. 0,65           C. 0,58          D. 0,52

9.Hasil dari 8 ¹/₃ : 2 ²/₉ – ³/₄ x ( -²/₁₅) adalah….

   A. 7 ⁷/₁₀       B. 6 ⁷/₂₀         C. 4 ¹³/₂₀       D. 3 ¹⁷/₂₀

10. Pak Ahmad memiliki tanah seluas 24 ha. tanah tersebut ditanami pohon mangga  ¹/₃ bagian, ditanami jeruk ¹/₄ bagian, dan ¹/₆ bagian untuk kolam ikan dan sisanya ingin ditanami berbagai tanaman obat. Berapa luas tanah yang akan ditanami tanaman obat?

   A. 6 ha          B. 7,2 ha        C. 8 ha           D. 9 ha

11. Koefisien dari 5x² – 2x + 7 adalah....

   A.  x², x dan 1                      C. 5, - 2 dan 7

   B.  5, - 2 dan x                     D. 5 dan – 2

12. Kelipatan persekutuan terkecil (KPK) dari  8a²b³ dan 12a⁴b² adalah....

   A.  24a²b²        B. 24a⁴b³         C. 24a⁶b5         D. 24a⁸b⁶

13. Hasil dari 4a – 2ab – (a – 5b) =….

   A. 4a – 7b                              C. 3a – 2ab – 5a

   B. 5a – 5b                              D. 3a – 2ab + 5b

14. Hasil dari 3 (x + 2y) – 2 (2x – 5y) = ….

    A. – x + 16y                          C. x – 16y

    B.  – 7x + 8y                         D. 7x + 8y

15.Dari pernyataan berikut, yang benar adalah....

   A.  a(b – c) = ac – bc             C. a ( b – c)  = ba – bc   

   B.  a (b – c) = cb – ca            D. a  (b – c) = ab – ac

16. Hasil dari (2x  + 3) (x – 5) adalah....

   A.  2x² – 7x – 15                   C. 2x² + 8x – 15

   B.  2x² + 7x – 15                   D. 2x² – 2x – 15

17. Hasil dari 12a²b³ : 4ab =....

   A.  3a³b²           B. 3ab²           C. 3a²b           D. 3a²b²

18. Diketahui X = {x | x ≤ 8, x є bilangan prima) dan Y = {x | - 2 ≤ x ≤ 5, x є bilangan bulat}, maka anggota (X ∩ Y) adalah ....
   A. {1, 2, 3, 5}                      C. {-1, 0, 1, 2, 3, 4}
   B. {2, 3,  5}                         D. {-1, 2, 3, 4, 5}

19. Diketahui : K = {x | -2 ≤ x ≤ 3; x є bilangan bulat} dan L = {x | 0 < x ≤ 5; x є bilangan ganjil}. Maka K – L adalah ....
   A. {-1, 0, 1, 2, 3}                 C. {-2, -1, 0, 2}
   B. {-1, 0, 1, 2}                     D. {2, 3, 5}

20. Diketahui B = {p,q,r,s}. Banyaknya himpunan bagian dari B adalah ....
   A. 4                B. 8               C. 16              D. 32

21. Jika n(S) = 155, n(P) = 100, n(Q) = 120 dan n (P ∩ Q)= 80, maka n(P ∪ Q)^c adalah....

   A. 15              B. 35              C. 55              D. 140

22. Dari 42 anak, terdapat 23  anak gemar makan permen dan 17 gemar makan coklat. Jika  9 anak tidak gemar makan permen dan coklat, maka banyaknya anak yang gemar makan coklat dan permen adalah .... anak.
   A. 5               B. 6                C. 7                D. 8

23. Suatu kelas  terdapat 30 anak. 15 anak suka menggambar, 20 anak suka menyanyi, dan 4 anak tidak suka kedua-duanya. Banyaknya anak yang  hanya suka menggambar adalah ....
   A. 6               B. 7                C. 8                D. 9

24. Pernyataan di bawah ini yang bukan persamaan linear satu variabel adalah....

   A. a + 2 = 6                          C. x – 21 = 8x                    

   B.  y + 8 = 4y – 6                   D. 3x – y = 10

Penyelesaian PLDV

Hari/tgl : Kamis, 28 Nopember 2019
Kelas : VII E & VII F

Menyelesaikan PLSV

Persamaan adalah suatu pernyataan matematika dalam bentuk simbol yang menyatakan bahwa dua hal adalah persis sama. Dari bentuk-bentuk 3(x – 1) + x dan –x + 7, kita dapat membentuk persamaan

yang merupakan suatu persamaan linear satu variabel (PLSV). Untuk menyelesaikan suatu persamaan, kita harus menentukan nilai dari x sedemikian sehingga persamaan tersebut menjadi benar, yang berarti, nilai dari ruas kiri sama dengan ruas kanan. Perhatikan tabel berikut.

Berdasarkan tabel di atas, kita dapat menemukan bahwa persamaan 3(x – 1) + x = –x + 7 akan bernilai benar ketika kita mengganti x dengan bilangan 2, dan akan salah jika kita mengganti x dengan bilangan selain 2. Bilangan pengganti yang dapat menyebabkan suatu persamaan bernilai benar disebut selesaian atau akar.

Menyelesaikan persamaan dengan menggunakan tabel akan memakan waktu yang cukup lama. Untuk itu, kita dapat menuliskan suatu persamaan yang diberikan ke dalam persamaan ekuivalen yang lebih sederhana, sampai kita mendapatkan solusi yang diminta. Persamaan-persamaan yang ekuivalen adalah persamaan-persamaan yang memiliki himpunan selesaian sama, dan diperoleh dari penyederhanaan kedua ruas persamaan dengan menggunakan sifat-sifat penjumlahan, perkalian, dan distributif dari suatu persamaan, sampai diperoleh suatu persamaan dalam bentuk x = konstanta.

Sifat Penjumlahan dan Perkalian Suatu Persamaan
Jika A, B, dan C merupakan bentuk-bentuk aljabar dan A = B, maka A + C = B + C, AC = BC, dan A/C = B/C (C ≠ 0).

Dengan kata lain, berdasarkan sifat penjumlahan suatu persamaan, kita dapat menambahkan suatu bilangan atau bentuk aljabar lain ke dalam ruas kanan dan kiri persamaan tersebut. Pernyataan yang serupa dapat dibuat untuk menyatakan sifat perkalian suatu persamaan. Sifat-sifat dari persamaan ini dapat dikombinasikan untuk dijadikan panduan dalam menyelesaikan suatu persamaan linear. Sebagai catatan, tidak semua langkah dalam panduan ini diperlukan dalam menyelesaikan setiap persamaan.

Berikut ini merupakan panduan/langkah-langkah dalam menyelesaikan persamaan linear satu variabel.

Hilangkan tanda kurung dengan menggunakan sifat distributif, kemudian operasikan suku-suku yang serupa.

Gunakan sifat penjumlahan suatu persamaan untuk menulis persamaan tersebut sehingga semua variabel berada di satu ruas, sedangkan semua konstanta berada di ruas lainnya. Sederhanakan masing-masing ruas.

Gunakan sifat perkalian suatu persamaan untuk menghasilkan persamaan yang berbentuk x = konstanta.

Untuk soal penerapan, jawablah ke dalam kalimat sempurna dan gunakan satuan yang sesuai dengan perintah.

Sebagai contoh pertama, kita akan mencoba menyelesaikan persamaan 3(x – 1) + x = –x + 7 yang merupakan masalah di awal pembahasan ini.

Contoh 1: Menyelesaikan PLSV dengan Menggunakan Sifat-sifat Persamaan

Selesaikan persamaan 3(x – 1) + x = –x + 7.

Pembahasan

Seperti selesaian dengan menggunakan tabel, kita juga memperoleh bahwa selesaian dari persamaan tersebut adalah x = 2.

Sumber : https://yos3prens.wordpress.com

Penyelesaian SPLDV

Hari,tgl : Rabu, 27 Nopember 2019

Kelas : VIII A

METODE GABUNGAN UNTUK MENYELESAIKAN SISTEM PERSAMAAN LINEAR (SPLDV)

Dalam materi Sistem Persamaan Linear Dua Variabel, sebelumnya kita sudah pernah membahas dua metode yang bisa dipakai untuk menentukan himpunan penyelesaian SPLDV, yang akan dibahas kali ini yaitu metode gabungan. Metode gabungan adalah suatu metode yang digunakan untuk menentukan himpunan penyelesaian suatu SPLDV dengan cara menggunakan dua metode sekaligus yakni metode eliminasi dan metode substitusi.
Pertama bisa menggunakan metode eliminasi untuk mencari salah satu nilai variabel. Langkah berikutnya setelah nilai variabel didapatkan, maka nilai variabel tersebut kita substitusikan untuk mendapatkan variabel yang lain. Supaya lebih paham kita bahas bersama-sama contoh soal di bawah ini.

CONTOH 1

Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel x + 2y = 6 dan 2x – y = 6 dengan menggunakan metode gabungan!
x + 2y = 6………….(1)
2x – y = 6………….(2)
Langkah I eliminasi salah satu variabel
Pertama kita harus mengeliminasi variabel x

x + 2y = 6	x 2	2x + 4y = 12
2x – y = 6	x 1	2x – 2y =   6   –
		6y   = 6
		y = 1

Dari langkah I diperoleh y = 1
Selanjutnya untuk memperoleh nilai x, substitusikan nilai y = 1 ke persamaan (1)
yaitu x + 2y = 6
x + 2(1) = 6
=> x + 2 = 6
=> x = 6 – 2
=> x = 4
Jadi, himpunan penyelesaian dari SPLDVdari persamaan x + 2y = 6 dan 2x – y = 6
adalah {(4, 1)}.

Penyelesaian SPLDV Metode Eliminasi

Hari/tgl : Jumat, 15 Nopember 2019
Kelas : VIII A

3. Penyelesaian SPLDV Metode Eliminasi

Langkah – langkah menyelesaikan spldv dengan metode eliminasi :

Metode eliminasi adalah Metode atau cara untuk menyelesaikan sistem persamaan linier dua variabel dengan cara mengeliminasi atau menghilngkan salah satu peubah (variabel) dengan menyamakan koefisien dari persamaan tersebut.

Cara untuk menghilangkan salah satu peubahnya yaitu dengan cara perhatikan tandanya, apabila tandanya sama [(+) dengan (+) atau (-) dengan (-) ] , maka untuk mengeliminasinya dengan cara mengurangkan. Dan sebaliknya apabila tandanya berbeda maka gunakanlah sistem penjumlahan.

Untuk lebih jelasnya tentang langkah – langkah diatas maka perhatikan contoh soal spldv eliminasi di bawah ini :

Contoh Soal SPLDV Eliminasi 1

1. Tentukan Himpunan penyelesaian dari persamaan x + 3y = 15 dan 3x + 6y = 30

Penyelesaian :

Diketahui :

Persamaan 1 = x + 3y = 15
Persamaan 2 = 3x + 6y = 30

Langkah Pertama yaitu menentukan variabel mana yang akan di eliminasi terlebih dahulu. Kali ini kita akan menghilangkan x terlebih dahulu, dan supaya kita temukan nilai y . Caranya yaitu :

3x + 6y = 30    : 3
x + 2y = 10 . . . . ( 1 )
x + 3y = 15 . . . .(2)

Langkah Kedua Dari persamaan (1) dan (2), mari kita eliminasi, sehingga hasilnya :

x + 3y = 15
x + 2y = 10     _
y = 5

Langkah Ketiga Selanjutnya, untuk mengetahui nilai x , maka caranya sebagai berikut :

x + 3y    = 15  | x2 | <=> 2x + 6y = 30   . . . .( 3 )
3x + 6y = 30  | x1 | <=> 3x + 6y = 30  . . .. (4 )

Eliminasi antara persamaan (3) dengan (4 ), yang hasilnya menjadi :

3x + 6y = 30
2x + 6y = 30   _
x = 0

Maka, Himpunan penyelesaiannya adalah HP = { 0 . 5 }

Contoh Soal SPLDV Eliminasi 2

2. Tentukan Penyelesaian dari persamaan  3x+ 5y = 16 , dan 4x + y = 10 , jika x = a dan y = b . Maka tentukan nilai a dan b !

Penyelesaian :

Diketahui :

Persamaan 1 = 3x+ 5y = 16
Persamaan 2 = 4x + y = 10

Langkah Pertama yaitu tentukan variabel mana yang akan di eliminasi terlebih dahulu perhatikan penyelesaian di bawah ini :

3x+ 5y = 16  | x1 | <=> 3x + 5y = 16 . . . .( 1 )
4x + y = 10 | x5 | <=> 20x + 5y = 50 . . .  ( 2 )

Dari persamaan (1 ) dan (2 ), dapat kita eliminasi dan menghasilkan :

20x + 5y = 50
3x + 5y = 16     _
17 x + 0 = 34
x = 34 / 17
x = 2

Langkah Kedua Selanjutnya, lakukan langkah yang sama namun kali ini yang harus sama x nya , maka caranya adalah :

3x+ 5y = 16 | x4 | <= > 12 x + 20y = 64 . . .(3)

4x + y = 10 | x3 | <=> 12x + 3y =  30 . . . .(4)

Langkah Ketiga Persamaan (3) dan (4) , mari kita eliminasi untuk menghasilkan nilai y :

12 x + 20y = 64
12x + 3y =  30     _
0 + 17y = 34
y = 2

Jadi , HP ={ 2 ,2 } , dan nilai a dan b adalah :

a= x = 2 dan b = y = 2

Menyelesaian PLSV

Hari/tgl : Kamis, 14 Nopember 2019
Kelas : VII E & VII F

Menyelesaikan PLSV

Persamaan adalah suatu pernyataan matematika dalam bentuk simbol yang menyatakan bahwa dua hal adalah persis sama. Dari bentuk-bentuk 3(x – 1) + x dan –x + 7, kita dapat membentuk persamaan

yang merupakan suatu persamaan linear satu variabel (PLSV). Untuk menyelesaikan suatu persamaan, kita harus menentukan nilai dari x sedemikian sehingga persamaan tersebut menjadi benar, yang berarti, nilai dari ruas kiri sama dengan ruas kanan. Perhatikan tabel berikut.

Berdasarkan tabel di atas, kita dapat menemukan bahwa persamaan 3(x – 1) + x = –x + 7 akan bernilai benar ketika kita mengganti x dengan bilangan 2, dan akan salah jika kita mengganti x dengan bilangan selain 2. Bilangan pengganti yang dapat menyebabkan suatu persamaan bernilai benar disebut selesaian atau akar.

Menyelesaikan persamaan dengan menggunakan tabel akan memakan waktu yang cukup lama. Untuk itu, kita dapat menuliskan suatu persamaan yang diberikan ke dalam persamaan ekuivalen yang lebih sederhana, sampai kita mendapatkan solusi yang diminta. Persamaan-persamaan yang ekuivalen adalah persamaan-persamaan yang memiliki himpunan selesaian sama, dan diperoleh dari penyederhanaan kedua ruas persamaan dengan menggunakan sifat-sifat penjumlahan, perkalian, dan distributif dari suatu persamaan, sampai diperoleh suatu persamaan dalam bentuk x = konstanta.

Sifat Penjumlahan dan Perkalian Suatu Persamaan
Jika A, B, dan C merupakan bentuk-bentuk aljabar dan A = B, maka A + C = B + C, AC = BC, dan A/C = B/C (C ≠ 0).

Dengan kata lain, berdasarkan sifat penjumlahan suatu persamaan, kita dapat menambahkan suatu bilangan atau bentuk aljabar lain ke dalam ruas kanan dan kiri persamaan tersebut. Pernyataan yang serupa dapat dibuat untuk menyatakan sifat perkalian suatu persamaan. Sifat-sifat dari persamaan ini dapat dikombinasikan untuk dijadikan panduan dalam menyelesaikan suatu persamaan linear. Sebagai catatan, tidak semua langkah dalam panduan ini diperlukan dalam menyelesaikan setiap persamaan.

Berikut ini merupakan panduan/langkah-langkah dalam menyelesaikan persamaan linear satu variabel.

Hilangkan tanda kurung dengan menggunakan sifat distributif, kemudian operasikan suku-suku yang serupa.

Gunakan sifat penjumlahan suatu persamaan untuk menulis persamaan tersebut sehingga semua variabel berada di satu ruas, sedangkan semua konstanta berada di ruas lainnya. Sederhanakan masing-masing ruas.

Gunakan sifat perkalian suatu persamaan untuk menghasilkan persamaan yang berbentuk x = konstanta.

Untuk soal penerapan, jawablah ke dalam kalimat sempurna dan gunakan satuan yang sesuai dengan perintah.

Sebagai contoh pertama, kita akan mencoba menyelesaikan persamaan 3(x – 1) + x = –x + 7 yang merupakan masalah di awal pembahasan ini.

Contoh 1: Menyelesaikan PLSV dengan Menggunakan Sifat-sifat Persamaan

Selesaikan persamaan 3(x – 1) + x = –x + 7.

Pembahasan

Seperti selesaian dengan menggunakan tabel, kita juga memperoleh bahwa selesaian dari persamaan tersebut adalah x = 2.

Sumber : https://yos3prens.wordpress.com

Penyelesaian SPLDV Metode Substitusi

Cara Menentukan Penyelesaian SPLDV Metode Subtitusi

Kelas : VIII B
Hari/tgl : Selasa, 12 Nopember 2019

kita akan membahas tentang cara menentukan himpunan penyelesaian (HP) sistem persamaan linear dua variabel dengan menggunakan metode subtitusi. Adapun langkah-langkah untuk menyelesaikan SPLDV dengan metode subtitusi adalah sebagai berikut.

Langkah 1:

Pilihlah salah satu persamaan (jika ada pilih yang paling sederhana), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x.

Langkah 2:

Subtitusikan nilai x atau y yang diperoleh dari langkah 1 ke persamaan yang lain.

Agar kalian lebih memahami bagaimana caranya menentukan himpunan penyelesaian SPLDV dengan menggunakan metode subtitusi, silahkan kalian pelajari beberapa contoh soal dan pembahasannya berikut ini.

Contoh Soal #1

Carilah himpunan penyelesaian dari tiap SPLDV berikut ini.

5x + 5y = 25

3x + 6y = 24

Jawab

5x + 5y = 25 ………. Pers. (1)

3x + 6y = 24 ………. Pers. (2)

Dari persamaan (1) kita peroleh persamaan y sebagai berikut.

⇔ 5x + 5y = 25

⇔ 5y = 25 – 5x

⇔ y = 5 – x

Lalu kita subtitusikan persamaan y ke persamaan (2) sebagai berikut.

⇔ 3x + 6(5 – x) = 24

⇔ 3x + 30 – 6x = 24

⇔ 30 – 3x = 24

⇔ 3x = 30 – 24

⇔ 3x = 6

⇔ x = 2

Terakhir, untuk menentukan nilai y, kita subtitusikan nilai x ke persamaan (1) atau persamaan (2) sebagai berikut.

⇔ 5(2) + 5y = 25

⇔ 10 + 5y = 25

⇔ 5y = 25 – 10

⇔ 5y = 15

⇔ y = 3

Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {(2, 3)}.

Contoh Soal #2

Tentukan himpunan penyelesaian untuk SPLDV berikut ini dengan menggunakan metode subtitusi:

x – 2y = 8

3x + 2y = -8

Jawab

x – 2y = 8 ….………. Pers. (3)

3x + 2y = -8 ………. Pers. (4)

Dari persamaan (3) kita peroleh persamaan x sebagai berikut.

⇔ x – 2y = 8

⇔ x = 8 + 2y

Lalu kita subtitusikan persamaan x ke dalam persamaan (4) sebagai berikut.

⇔ 3(8 + 2y) + 2y = -8

⇔ 24 + 6y + 2y = -8

⇔ 24 + 8y = -8

⇔ 8y = -8 – 24

⇔ 8y = -32

⇔ y = -4

Terakhir, untuk menentukan nilai x, kita subtitusikan nilai y ke persamaan (3) atau persamaan (4) sebagai berikut.

⇔ 3x + 2(-4) = -8

⇔ 3x + (-8) = -8

⇔ 3x = -8 + 8

⇔ 3x = 0

⇔ x = 0

Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {(0, -4)}.

Penyelesaian SPLDV Metode Substitusi

Cara Menentukan Penyelesaian SPLDV Metode Subtitusi

Kelas : VIII A
Hari/tgl : Jumat, 08 Nopember 2019

kita akan membahas tentang cara menentukan himpunan penyelesaian (HP) sistem persamaan linear dua variabel dengan menggunakan metode subtitusi. Adapun langkah-langkah untuk menyelesaikan SPLDV dengan metode subtitusi adalah sebagai berikut.

Langkah 1:

Pilihlah salah satu persamaan (jika ada pilih yang paling sederhana), kemudian nyatakan x sebagai fungsi y atau y sebagai fungsi x.

Langkah 2:

Subtitusikan nilai x atau y yang diperoleh dari langkah 1 ke persamaan yang lain.

Agar kalian lebih memahami bagaimana caranya menentukan himpunan penyelesaian SPLDV dengan menggunakan metode subtitusi, silahkan kalian pelajari beberapa contoh soal dan pembahasannya berikut ini.

Contoh Soal #1

Carilah himpunan penyelesaian dari tiap SPLDV berikut ini.

5x + 5y = 25

3x + 6y = 24

Jawab

5x + 5y = 25 ………. Pers. (1)

3x + 6y = 24 ………. Pers. (2)

Dari persamaan (1) kita peroleh persamaan y sebagai berikut.

⇔ 5x + 5y = 25

⇔ 5y = 25 – 5x

⇔ y = 5 – x

Lalu kita subtitusikan persamaan y ke persamaan (2) sebagai berikut.

⇔ 3x + 6(5 – x) = 24

⇔ 3x + 30 – 6x = 24

⇔ 30 – 3x = 24

⇔ 3x = 30 – 24

⇔ 3x = 6

⇔ x = 2

Terakhir, untuk menentukan nilai y, kita subtitusikan nilai x ke persamaan (1) atau persamaan (2) sebagai berikut.

⇔ 5(2) + 5y = 25

⇔ 10 + 5y = 25

⇔ 5y = 25 – 10

⇔ 5y = 15

⇔ y = 3

Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {(2, 3)}.

Contoh Soal #2

Tentukan himpunan penyelesaian untuk SPLDV berikut ini dengan menggunakan metode subtitusi:

x – 2y = 8

3x + 2y = -8

Jawab

x – 2y = 8 ….………. Pers. (3)

3x + 2y = -8 ………. Pers. (4)

Dari persamaan (3) kita peroleh persamaan x sebagai berikut.

⇔ x – 2y = 8

⇔ x = 8 + 2y

Lalu kita subtitusikan persamaan x ke dalam persamaan (4) sebagai berikut.

⇔ 3(8 + 2y) + 2y = -8

⇔ 24 + 6y + 2y = -8

⇔ 24 + 8y = -8

⇔ 8y = -8 – 24

⇔ 8y = -32

⇔ y = -4

Terakhir, untuk menentukan nilai x, kita subtitusikan nilai y ke persamaan (3) atau persamaan (4) sebagai berikut.

⇔ 3x + 2(-4) = -8

⇔ 3x + (-8) = -8

⇔ 3x = -8 + 8

⇔ 3x = 0

⇔ x = 0

Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {(0, -4)}.

Penyelesaian SPLDV Metode Grafik

Kelas : VIII B

Hari/tgl : Kamis, 07 Nopember 2019

Penyelesaian SPLDV

1. Metode Grafik

Penyelesaian SPLDV dengan metode grafik dilakukan dengan menentukan koordinat titik potong dari kedua garis yang mewakili kedua persamaan linear. Sebelumnya, sobat idschool perlu belajar mengenai cara menggambar garis pada persamaan linear terlebih dahulu.

Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:

Menggambar garis yang mewakili kedua persamaan dalam bidang kartesius.

Menemukan titik potong dari kedua grafik tersebut.

Penyelesaiannya adalah (x, y).

Perhatikan kembali dua persamaan yang digunakan pada metode – metode sebelumnya, yaitu:

2x + 3y = 8 persamaan (i)

3x + y = 5 persamaan (ii)

Berikut ini penyelesaian SPLDV dengan metode grafik.

Langkah 1: menggambar kedua grafik

Menentukan titik potong pada kedua sumbu x dan y dari kedua persamaan.

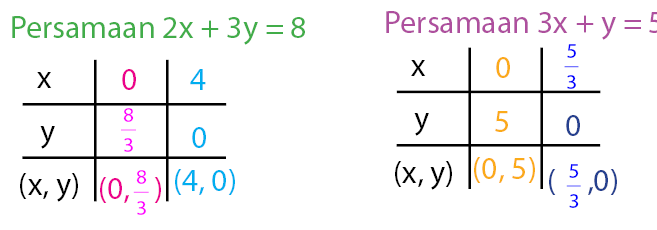
Gambar garis lurus untuk kedua persamaan linear dalam bidang kartesius diberikan seperti gambar di bawah.

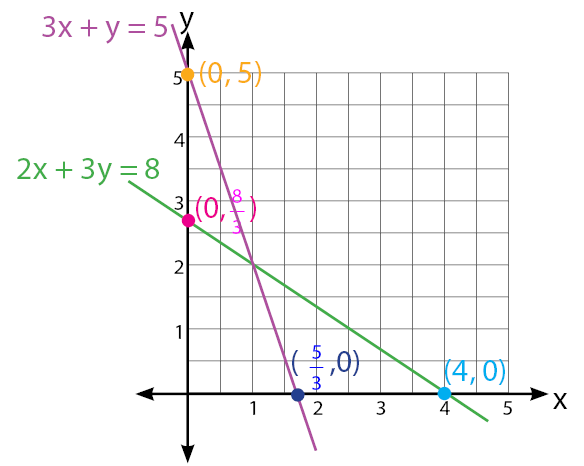
Langkah 2: menemukan titik potong dari kedua grafik tersebut.

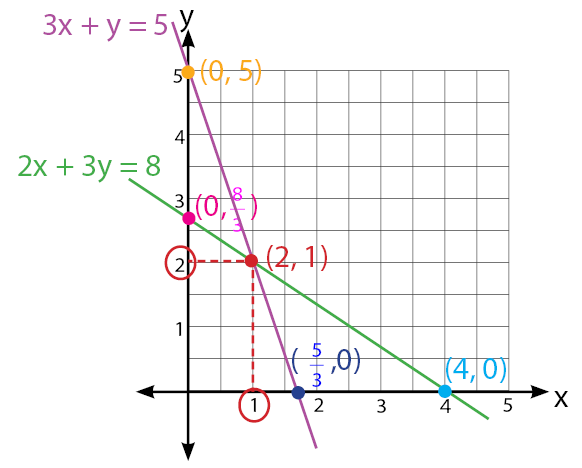
Langkah 3: penyelesaiannya adalah (x, y)

Berdasarkan gambar dapat diketahui bahwa titik potong berada pada x = 1 dan y = 2, jadi penyelesaiannya adalah (1, 2).

Persamaan Linear Satu Variabel

Kelas  : VII G

Hari/tgl : Senin, 04 Nopember 2019

Persamaan Linear Satu Variabel (PLSV)

1. Pengertian Persamaan Linear Satu Variabel

Perhatikan kalimat-kalimat terbuka di bawah ini.
a. x – 3 = 5
b. p2 + 4 = 8
c.5n/6 =15

Kalimat-kalimat terbuka di atas menggunakan tanda hubung ” = ” (sama dengan). Kalimat-kalimat seperti ini disebut persamaan.

Persamaan-persamaan tersebut mempunyai satu variabel (peubah), yaitu x, p, dan n di mana derajat dari masing-masing variabel adalah 1, maka persamaan seperti itu disebut persamaan linear satu variabel. 

Bentuk umum PLSV adalah ax + b = 0

2. Sifat-Sifat PLSV

Misalkan A = B adalah persamaan linear dengan variabel x dan c adalah konstanta bukan nol. Persamaan A = B ekuivalen dengan persamaan-persamaan berikut:
1. A + C = B + C
2. A – C = B – C
3. A x C = B x C
4. A : C = B : C, C ¹ 0

Sumber : berpendidikan.com