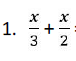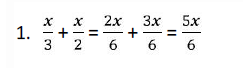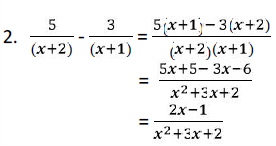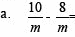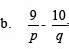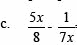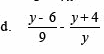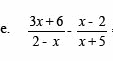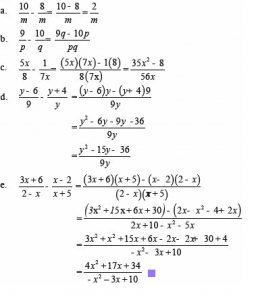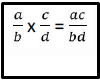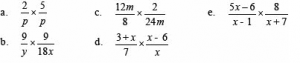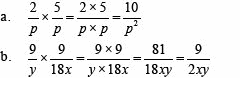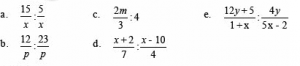Selasa, 29 Oktober 2019
Sistem Persamaan Linear Dua Variabel (SPLDV)
Hari/tgl : Rabu, 30 Oktober 2019
![\[ 2x^{2} + 5x = 14 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-aa2d0c8b2c054be7b976afa0b40cb77e_l3.svg "Rendered by QuickLaTeX.com")
![\[ \frac{1}{x} + \frac{1}{y} = 2 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0bc301d286d04816235e4440708c340f_l3.svg "Rendered by QuickLaTeX.com")
![\[2x + 5y = 14\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3105d808d8a6b3e2a50871b5337b882f_l3.svg "Rendered by QuickLaTeX.com")
![\[3a + 4b =24\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-1b6a5e77a2ce98465c9267c37db01b5d_l3.svg "Rendered by QuickLaTeX.com")
![\[q + r = 3\]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5dd9b1303efc5b55762a26b117d39718_l3.svg "Rendered by QuickLaTeX.com")
![\[ ax + by = c \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-272f2689cca0037682261444da8b2d10_l3.svg "Rendered by QuickLaTeX.com")
- Metode Substitusi
- Metode Eliminasi
- Metode Gabungan
- Metode Grafik.
Senin, 28 Oktober 2019
Post Test Persamaan Garis Lurus
Hari/tgl : Selasa, 29 Oktober 2019
Topik : Gradien dan Persamaan Garis Lurus
Kelas : VIII B
(1) Titik A memiliki koordinat (8, −1) dan titik B (2, − 13). Gradien garis yang melalui titik A dan B adalah.....
A. − 3
B. −1/3
C. 1/2
D. 2
(2) Perhatikan gambar berikut ini!
Gadien garis p adalah.....
A. −3/2
B. −2/3
C. 2/3
D. 3/2
(3) Gradien garis yang memiliki persamaan y = 3x − 5 adalah.....
A. − 5
B. −5/3
C. 3
D. 5
(4) Gradien garis dengan persamaan 3x − 6y + 9 = 0 adalah....
A. − 2
B. −1/2
C. 1/2
D. 2
(5) Gradien garis dengan persamaan 2x + 8y − 5 = 0 adalah....
A. − 4
B. −1/4
C. 1/4
D. 4
(6) Gradien garis m adalah....
A. − 3/2
B. −2/3
C. 2/3
D. 3/2
(7) Persamaan suatu garis yang melalui titik (2, 3) dan titik (3, 5) adalah....
A. y = 2x + 1
B. y = 2x − 1
C. y = − 2x − 1
D. y = − 2x + 1
(8) Persamaan garis yang melalui titik (2, 3) dan memiliki gradien sebesar 1/2 adalah....
A. x − 2y + 4 = 0
B. x − 2y − 8 = 0
C. 2x − y + 4 = 0
D. 2x − y − 8 = 0
(9) Garis l melalui titik (1, 1) dan sejajar dengan garis m yang memiliki persamaan 3x − 2y + 8 = 0. Persamaan garis l adalah....
A. − 3x − 2y − 1 = 0
B. 3x + 2y − 1 = 0
C. 3x − 2y − 1 = 0
D. − 3x + 2y − 8 = 0
(10) Garis g melalui titik (2, 2) dan tegal lurus terhadap garis m yang memiliki persamaan y = 3x − 4. Persamaan garis g adalah....
A. 3x + y + 8 = 0
B. 3x + y − 8 = 0
C. x + 3y + 8 = 0
D. x + 3y − 8 = 0
(11) Persamaan garis pada gambar berikut adalah....
A. y = 2x + 3
B. y = − 2x − 3
C. y = 3x + 2
D. y = − 3x + 2
(12) Garis h tegak lurus garis m : 5x − 2y + 3 = 0. Gradien dari garis h adalah....
A. − 5/2
B. − 2/5
C. 2/5
D. 5/2
@Bank Soal Matematikastudycenter.com*
Rabu, 23 Oktober 2019
Operasi Hitung Pecahan Aljabar
Kelas : VII E & VII F
Hari / tgl : Kamis, 24 Oktober 2019
Operasi Hitung Pecahan Bentuk Aljabar
Seperti dalam pecahan bentuk biasa , dalam pecahan bentuk aljabar juga ada 4 operasi hitung yaitu :
Penjumlahan pecahan bentuk aljabar
Pengurangan pecahan bentuk aljabar
Perkalian pecahan bentuk aljabar
Pembagian pecahan bentuk aljabar
Untuk lebih jelasnya , perhatikan penjelasan di bawah ini :
1. Penjumlahan Dan Pengurangan Pecahan Bentuk Aljabar
Untuk menyelesaikan pecahan bentuk aljabar , prinsipnya sama dengan menyelesaikan penjumlahan pecahan biasa yaitu dengan cara menyamakan penyebutnya terlebih dahulu baru di jumlahkan atau dikurangkan .
Perhatikan contoh – contoh di bawah ini :
Sederhanakan benuk pecahan aljabar berikut
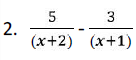
Penyelesaian:
Selesaikan bentuk pecahan aljabar berikut ini :
Penyelesaian :
2. Perkalian Dan Pembagian Pecahan Bentuk Aljabar
a. Perkalian Pecahan Bentuk Aljabar
Cara untuk menyelesaiakan operasi hitung pecahan bentuk aljabar prisnsipnya sama dengan perkalian pecahan bentuk biasa . Yaitu dengan cara mengalikan pembilang dengan pembilang dan mengalikan penyebut dengan penyebut .
Rumus :
Untuk lebih jelasnya , perhatikan contoh di bawah ini :
Sederhanakan perkalian pecahan bentuk aljabar berikut
Penyelesaian :
b. Pembagian Pecahan Bentuk Aljabar
Untuk menyelesaiakan pembagian pecahan bentuk aljabar , caranya sama dengan menyelesaikan pembagian pecahan biasa , yaitu dengan cara merubah ke bentuk perkalian dimana bilangan kedua dibalik, penyebut menjadi pembilang dan pembilang menjadi penyebut .
Rumus
Supaya lebih jelas lagi , perhatikan contoh di bawah ini :
Sederhanakan bentuk pembagian pecahan aljabar berikut :
Penyelesaian:
Sumber : rumusrumus.com
Selasa, 22 Oktober 2019
Titik Potong Pada Dua Garis Lurus
Kelas : VIII A
Hari/tgl : Rabu, 23 Oktober 2019
perhatikan gambar di bawah ini.
Pada gambar di atas tampak dua buah garis yang tidak sejajar yaitu garis k dengan persamaan garis y1 = m1x + c1 dan garis l dengan persamaan garis y2 = m2x + c2. Kita ketahui bahwa bahwa dua garis yang tidak saling sejajar akan berpotongan di satu titik tertentu. Jika kedua garis ini berpotongan di titik P(xo, yo) maka berlaku:
yo = m1xo + c1 . . . (*)
yo = m2xo + c2 . . . .(**)
Dari persamaan * dan **, akan diperoleh:
m1xo + c1 = m2xo + c2
m1xo – m2xo = c2 – c1
x0 = (c2 – c1)/(m1 – m2)
Selanjutnya, untuk memperoleh nilai yo, substitusikan nilai xo pada
salah satu persamaan garisnya.
Jadi, jika y1 = m1x + c1 dan y2 = m2x + c2 adalah persamaan dua garis yang tidak saling sejajar maka titik potongnya dapat dicari dengan menyelesaikan persamaan m1x + c1 = m2x + c2, kemudian menyubstitusikan nilai x ke salah satu persamaan garis tersebut.
Untuk memantapkan pemahaman Anda tentang cara menentukan titik potong dua buah garis, silahkan simak contoh soal di bawah ini.
Contoh Soal 1
Tentukan titik potong kedua garis dengan persamaan y = x + 1 dan y = –5x + 3
Penyelesaian:
Karena kedua persamaan sudah berbentuk y = mx + c, maka titik potong untuk nilai x dapat di cari dengan menghilangkan variabel y, yakni:
<=> x +1 = –5x + 3
<=> x + 5x = 3 – 1
<=> 6x = 2
<=> x = 2/6
<=> x = 1/3
Selanjutnya, untuk menentukan nilai y substitusikan nilai x ke persamaan maka y = x + 1, maka:
<=> y = x + 1
<=> y = 1/3 + 1
<=> y = 1/3 + 3/3
<=> y = 4/3
Jadi, titik potong garis dengan persamaan y = x + 1 dan y = –5x + 3 adalah (1/3, 4/3).
Contoh Soal 2
Tentukan titik potong kedua garis dengan persamaan 3x + 5y = 2 dan 2x – y = 3.
Penyelesaian:
Ubah persamaan 3x + 5y = 2 ke bentuk y = mx + c, yakni:
<=> 3x + 5y = 2
<=> 5y = –3x + 2
<=> y = (–3x + 2)/5
<=> y = (–3/5)x + 2/5
Ubah juga persamaan 2x – y = 3 ke bentuk y = mx + c, yakni:
<=> 2x – y = 3
<=> 2x– 3 = y
<=> y = 2x– 3
maka titik potong untuk x dapat di cari dengan menghilangkan variabel y, yakni:
<=> (–3/5)x + 2/5 = 2x– 3
<=> (–3/5)x – 2x = – 3 – 2/5
<=> (–3/5)x – (10/5)x = – 15/5 – 2/5, jika kedua ruas dikalikan 5 maka:
<=> – 3x – 10x = – 15 – 2
<=> –13x = – 17
<=> x = – 17/–13
<=> x = 17/13
Selanjutnya, untuk menentukan nilai y substitusikan nilai x ke persamaan maka y = 2x– 3, maka:
<=> y = 2x– 3
<=> y = 2(17/13)– 3
<=> y = 34/13 – 3
<=> y = 34/13 – 39/13
<=> y = –5/13
Jadi, titik potong garis dengan persamaan 3x + 5y = 2 dan 2x – y = 3 adalah (17/13, –5/13).
Sumber : mafia.mafiaol.com
Senin, 21 Oktober 2019
Titik Potong Pada Dua Garis
Kelas : VIII B
Hari/tgl : Selasa, 22 Oktober 2019
perhatikan gambar di bawah ini.
Pada gambar di atas tampak dua buah garis yang tidak sejajar yaitu garis k dengan persamaan garis y1 = m1x + c1 dan garis l dengan persamaan garis y2 = m2x + c2. Kita ketahui bahwa bahwa dua garis yang tidak saling sejajar akan berpotongan di satu titik tertentu. Jika kedua garis ini berpotongan di titik P(xo, yo) maka berlaku:
yo = m1xo + c1 . . . (*)
yo = m2xo + c2 . . . .(**)
Dari persamaan * dan **, akan diperoleh:
m1xo + c1 = m2xo + c2
m1xo – m2xo = c2 – c1
x0 = (c2 – c1)/(m1 – m2)
Selanjutnya, untuk memperoleh nilai yo, substitusikan nilai xo pada
salah satu persamaan garisnya.
Jadi, jika y1 = m1x + c1 dan y2 = m2x + c2 adalah persamaan dua garis yang tidak saling sejajar maka titik potongnya dapat dicari dengan menyelesaikan persamaan m1x + c1 = m2x + c2, kemudian menyubstitusikan nilai x ke salah satu persamaan garis tersebut.
Untuk memantapkan pemahaman Anda tentang cara menentukan titik potong dua buah garis, silahkan simak contoh soal di bawah ini.
Contoh Soal 1
Tentukan titik potong kedua garis dengan persamaan y = x + 1 dan y = –5x + 3
Penyelesaian:
Karena kedua persamaan sudah berbentuk y = mx + c, maka titik potong untuk nilai x dapat di cari dengan menghilangkan variabel y, yakni:
<=> x +1 = –5x + 3
<=> x + 5x = 3 – 1
<=> 6x = 2
<=> x = 2/6
<=> x = 1/3
Selanjutnya, untuk menentukan nilai y substitusikan nilai x ke persamaan maka y = x + 1, maka:
<=> y = x + 1
<=> y = 1/3 + 1
<=> y = 1/3 + 3/3
<=> y = 4/3
Jadi, titik potong garis dengan persamaan y = x + 1 dan y = –5x + 3 adalah (1/3, 4/3).
Contoh Soal 2
Tentukan titik potong kedua garis dengan persamaan 3x + 5y = 2 dan 2x – y = 3.
Penyelesaian:
Ubah persamaan 3x + 5y = 2 ke bentuk y = mx + c, yakni:
<=> 3x + 5y = 2
<=> 5y = –3x + 2
<=> y = (–3x + 2)/5
<=> y = (–3/5)x + 2/5
Ubah juga persamaan 2x – y = 3 ke bentuk y = mx + c, yakni:
<=> 2x – y = 3
<=> 2x– 3 = y
<=> y = 2x– 3
maka titik potong untuk x dapat di cari dengan menghilangkan variabel y, yakni:
<=> (–3/5)x + 2/5 = 2x– 3
<=> (–3/5)x – 2x = – 3 – 2/5
<=> (–3/5)x – (10/5)x = – 15/5 – 2/5, jika kedua ruas dikalikan 5 maka:
<=> – 3x – 10x = – 15 – 2
<=> –13x = – 17
<=> x = – 17/–13
<=> x = 17/13
Selanjutnya, untuk menentukan nilai y substitusikan nilai x ke persamaan maka y = 2x– 3, maka:
<=> y = 2x– 3
<=> y = 2(17/13)– 3
<=> y = 34/13 – 3
<=> y = 34/13 – 39/13
<=> y = –5/13
Jadi, titik potong garis dengan persamaan 3x + 5y = 2 dan 2x – y = 3 adalah (17/13, –5/13).
Sumber : mafia.mafiaol.com
Rabu, 16 Oktober 2019
Perkalian dan Pembagian Aljabar
Hari/tgl : Kamis, 17 Oktober 2019
Ingat kembali bahwa pada operasi perkalian bilangan bulat terdapat sifat distributif pada penjumlahan dan pengurangan, yaitu a(b + c)= ab + ac , dan a(b – c) = ab – ac. Pada operasi perkalian bentuk aljabar sifat tersebut juga berlaku.
Untuk melakukan operasi perkalian antara konstanta dengan bentuk aljabar, dapat dilakukan dengan mudah, yaitu dengan mengalikan konstanta tersebut dengan konstanta pada bentuk aljabar.
Contoh :
Seperti pada perkalian antara konstanta dengan bentuk aljabar, dalam perkalian dua bentuk aljabar berlaku juga sifat distributif. Untuk suku yang sejenis, jika variabel dikalikan maka akan menjadi pangkat, misal
, sedangkan konstanta dikalikan seperti biasa. Untuk suku yang tidak sejenis maka variabelnya akan dituliskan saja, dan konstanta dikalikan seperti biasa.Perkalian satu suku dengan dua suku,
Operasi pembagian pada bentuk aljabar dilakukan dengan cara membagi konstantanya seperti biasa, namun untuk variabelnya, dilihat dulu koefisien dari kedua variabel nya, kemudian bagi masing-masing variabelnya dengan koefisiennya.
Selasa, 15 Oktober 2019
Menentukan Persamaan Garis Lurus
Kelas : VIII A
Hari/tgl : 16 Oktober 2019
A. Pengertian Persamaan Garis Lurus
Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis.
Sedangkan garis lurus sendiri ialah kumpulan dari titik – titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
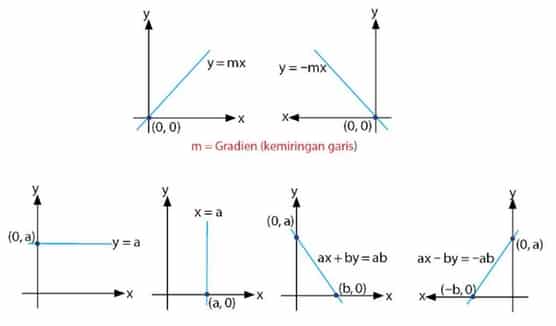
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
y = mx
y = -mx
y = a
x = a
ax + by = ab
ax – by = -ab
dan lain-lain
Perhatikan gambar dibawah ini beberapa contoh grafik dan bentuk garis lurus serta cara menyatakan atau menentukannya :
Contoh Cara Menentukan Persamaan Garis Lurus
Minggu, 13 Oktober 2019
Menentukan Persamaan Garis Lurus
Kelas : VIII C
Hari/tgl : 14 Oktober 2019
A. Pengertian Persamaan Garis Lurus
Persamaan Garis lurus yaitu suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis.
Sedangkan garis lurus sendiri ialah kumpulan dari titik – titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
y = mx
y = -mx
y = a
x = a
ax + by = ab
ax – by = -ab
dan lain-lain
Perhatikan gambar dibawah ini beberapa contoh grafik dan bentuk garis lurus serta cara menyatakan atau menentukannya :
Contoh Cara Menentukan Persamaan Garis Lurus
Rabu, 09 Oktober 2019
Senin, 07 Oktober 2019
Kisi Kisi PTS Matematika Kls 7
KISI-KISI SOAL PILIHAN GANDANo. KOMPETENSIMATERIINDIKATORINDIKATOR SOALNO. SOAL 13.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat.Bilangan3.1.1 Mengenal bilangan bulat Menentukan suhu ruangan dengan menggunakan garis bilangan. 123.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat.Bilangan3.1.1 Mengenal bilangan bulat Menyelesaikan operasi tambah, kurang, kali, bagi dan pangkat bilangan bulat termasuk operasi campuran233.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat.Bilangan3.1.4 Menentukan bilangan pecahan ( biasa, desimal dan persen)Menyelesaikan operasi tambah, kurang, kali, bagi dan pangkat bilangan bulat termasuk operasi campuran343.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat.Bilangan3.1.4 Menentukan bilangan pecahan ( biasa, desimal dan persen)Menentukan nilai dari pecahan senilai 453.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat.Bilangan3.1.5 Membandingkan bilangan pecahan Menentukan pernyataan yang benar dari perbandingan pecahan564.1 Menyelesaikan masalah yang berkaitan dengan urutan beberapa bilangan bulat dan pecahan (biasa, campuran, desimal, persenBilangan 4.1.2 Menyelesaikan urutan pada bilangan
Pecahan
Mengurutkan nilai pecahan dari terbesar ke terkecil (pecahan biasa, desimal dab persen)673.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasiBilangan 3.2.3 Memahami konsep penjumlahan dan pengurangan pecahanMenentukan hasil dari operasi penjumlahan pecahan783.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasiBilangan3.2.8 Menentukan FPB dari dua bilangan atau lebihMenyebutkan faktor dari suatu bilangan894.2 Menyelesaikan masalah yang berkaitan dengan operasi hitung bilangan bulat dan pecahanBilangan4.2.5 Menyelesaikan permasalahan yang berkaitan dengan KPK dari dua bilangan atau lebihMenyelesaikan KPK dari dua bilangan9103.3 Menjelaskan dan menentukan representasi bilangan dalam bentuk bilangan berpangkat bulat positif dan negatifBilangan Berpangkat3.1.3 Menjelaskan dan menentukan representasi bilangan dalam bentuk bilangan bulat berpangkat positif dan negatifMenentukan hasil pemangkatan bilangan bulat negatif10114.3 Menyelesaikan masalah yang berkaitan dengan bilangan dalam bentuk bilangan berpangkat bulat positif dan negatifBilangan Berpangkat4.3.1 Menyelesaikan masalah tentang membandingkan bilangan berpangkat bulat positif dan negatifMenyelesaikan hasil pemangkatan operasi bilangan bulat 11123.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual.Himpunan3.4.2. Menyebutkan anggota himpunan dan bukan anggota himpunan;Menentukan himpunan dan bukan himpunan12133.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual.Himpunan3.4.3. Menyajikan himpunan dengan menyebutkan anggotanyaMenyebutkan anggota dari suatu himpunan13143.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual.Himpunan3.4.5. Menyajikan himpunan dengan notasi pembentuk himpunanMenyatakan himpunan dengan notasi pembentuk himpunan14153.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual.Himpunan3.4.6. Menyatakan himpunan kosongMenentukan pernyataan yang merupakan himpunan kosong15163.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual.Himpunan3.4.9. Membaca diagram Venn dari suatu himpunanMembaca diagram venn unuk menentukan anggota himpunan 16174.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunanHimpunan4.4.3. Menyebutkan himpunan bagian dari suatu himpunanMenentukan pernyataan himpunan bagian17184.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunanHimpunan4.4.4. Menyatakan himpunan kuasa dari suatu himpunanMenentukan anggota himpunan kuasa18194.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunanHimpunan4.4.6. Menyatakan irisan dari dua himpunanMenentukan anggota irisan dari dua himpunan19204.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunan
Himpunan4.4.9. Menyelesaikan masalah kontekstual yang berkaitan dengan gabungan daridua himpunanMenentukan anggota gabungan dari dua himpunan20
Kamis, 03 Oktober 2019
KISI KISI PTS MTK KLS 7 URAIAN
| KISI-KISI SOAL URAIAN | |||||
| No. | KOMPETENSI | MATERI | INDIKATOR | INDIKATOR SOAL | NO. SOAL |
| 1 | 3.1 Menjelaskan dan menentukan urutan pada bilangan bulat (positif dan negatif) dan pecahan (biasa, campuran, desimal, persen) | Bilangan | 3.1.1 Mengenal bilangan bulat | Menyelesaikan operasi hitung penjumlahan bilangan positif dan negatif | 1 |
| 2 | 3.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasi | Bilangan | 3.2.2 Menjelaskan sifat komutatif, asosiatif, dan distributif operasi hitung perkalian dan pembagian yang melibatkan bilangan bulat | Menyelesaikan operasi hitung perkalian bilangan bulat | 2 |
| 3 | 4.2 Menyelesaikan masalah yang berkaitan dengan operasi hitung bilangan bulat dan pecahan | Bilangan | 4.2.4 Menyelesaikan masalah yang berkaitan dengan sifat komutatif, asosiatif, dan distributif operasi hitung perkalian dan pembagian yang melibatkan bilangan pecahan | Menyelesaikan operasi hitung pembagian bilangan pecahan | 3 |
| 4 | 3.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasi | Bilangan | 3.2.8 Menentukan FPB dari dua bilangan atau lebih | Menyebutkan faktor dari bilangan | 4 |
| 5 | 4.2 Menyelesaikan masalah yang berkaitan dengan operasi hitung bilangan bulat dan pecahan | Bilangan | 4.2.6 Menyelesaikan permasalahan yang berkaitan dengan FPB dari dua bilangan atau lebih | Menyelesaikan FPB dari dua bilangan atau lebih | 5 |
| 6 | 4.3 Menyelesaikan masalah yang berkaitan dengan
bilangan dalam bentuk bilangan berpangkat bulat positif dan negatif |
Bilangan | 4.3.1 Menyelesaikan masalah tentang membandingkan bilangan berpangkat bulat positif dan negatif | Menyelesaikan perkalian dan pembagian bilangan berpangkat | 6 |
| 7 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.5. Menyajikan himpunan dengan notasi pembentuk himpunan | Menyebutkan anggota himpunan berdasarkan notasi pembentuk himpunan | 7 |
| 8 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.5. Menyajikan himpunan dengan notasi pembentuk himpunan | Menyajikan himpunan dalam bentuk notasi pembentuk himpunan | 8 |
| 9 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.8. Menggambar diagram Venn dari suatu himpunan | Menggambar diagram venn | 9 |
| 10 | 4.4
Menyelesaikan masalah kontekstual yang
berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan
kosong, komplemen himpunan |
Himpunan | 4.4.3. Menyebutkan himpunan bagian dari suatu himpunan | Menyebutkan anggota himpunan bagian dari suatu himpunan | 10 |
KISI KISI PTS MTK KLS 7 PILGAN
| KISI-KISI SOAL PILIHAN GANDA | |||||
| No. | KOMPETENSI | MATERI | INDIKATOR | INDIKATOR SOAL | NO. SOAL |
| 1 | 3.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat. | Bilangan | 3.1.1 Mengenal bilangan bulat | Menentukan suhu ruangan dengan menggunakan garis bilangan. | 1 |
| 2 | 3.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat. | Bilangan | 3.1.1 Mengenal bilangan bulat | Menyelesaikan operasi tambah, kurang, kali, bagi dan pangkat bilangan bulat termasuk operasi campuran | 2 |
| 3 | 3.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat. | Bilangan | 3.1.4 Menentukan bilangan pecahan ( biasa, desimal dan persen) | Menyelesaikan operasi tambah, kurang, kali, bagi dan pangkat bilangan bulat termasuk operasi campuran | 3 |
| 4 | 3.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat. | Bilangan | 3.1.4 Menentukan bilangan pecahan ( biasa, desimal dan persen) | Menentukan nilai dari pecahan senilai | 4 |
| 5 | 3.1 Menyelesaikan operasi bilangan bulat dan mengenal sifat operasi bilangan bulat. | Bilangan | 3.1.5 Membandingkan bilangan pecahan | Menentukan pernyataan yang benar dari perbandingan pecahan | 5 |
| 6 | 4.1 Menyelesaikan masalah yang berkaitan dengan urutan beberapa bilangan bulat dan pecahan (biasa, campuran, desimal, persen | Bilangan | 4.1.2 Menyelesaikan urutan pada bilangan Pecahan |
Mengurutkan nilai pecahan dari terbesar ke terkecil (pecahan biasa, desimal dab persen) | 6 |
| 7 | 3.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasi | Bilangan | 3.2.3 Memahami konsep penjumlahan dan pengurangan pecahan | Menentukan hasil dari operasi penjumlahan pecahan | 7 |
| 8 | 3.2 Menjelaskan dan melakukan operasi hitung bilangan bulat dan pecahan dengan memanfaatkan berbagai sifat operasi | Bilangan | 3.2.8 Menentukan FPB dari dua bilangan atau lebih | Menyebutkan faktor dari suatu bilangan | 8 |
| 9 | 4.2 Menyelesaikan masalah yang berkaitan dengan operasi hitung bilangan bulat dan pecahan | Bilangan | 4.2.5 Menyelesaikan permasalahan yang berkaitan dengan KPK dari dua bilangan atau lebih | Menyelesaikan KPK dari dua bilangan | 9 |
| 10 | 3.3 Menjelaskan dan menentukan representasi bilangan dalam bentuk bilangan berpangkat bulat positif dan negatif | Bilangan Berpangkat | 3.1.3 Menjelaskan dan menentukan representasi bilangan dalam bentuk bilangan bulat berpangkat positif dan negatif | Menentukan hasil pemangkatan bilangan bulat negatif | 10 |
| 11 | 4.3 Menyelesaikan masalah yang berkaitan dengan bilangan dalam bentuk bilangan berpangkat bulat positif dan negatif | Bilangan Berpangkat | 4.3.1 Menyelesaikan masalah tentang membandingkan bilangan berpangkat bulat positif dan negatif | Menyelesaikan hasil pemangkatan operasi bilangan bulat | 11 |
| 12 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.2. Menyebutkan anggota himpunan dan bukan anggota himpunan; | Menentukan himpunan dan bukan himpunan | 12 |
| 13 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.3. Menyajikan himpunan dengan menyebutkan anggotanya | Menyebutkan anggota dari suatu himpunan | 13 |
| 14 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.5. Menyajikan himpunan dengan notasi pembentuk himpunan | Menyatakan himpunan dengan notasi pembentuk himpunan | 14 |
| 15 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.6. Menyatakan himpunan kosong | Menentukan pernyataan yang merupakan himpunan kosong | 15 |
| 16 | 3.4. Menjelaskan dan menyatakan himpunan, himpunan bagian, himpunan semesta, himpunan kosong, komplemen himpunan, menggunakan masalah kontekstual. | Himpunan | 3.4.9. Membaca diagram Venn dari suatu himpunan | Membaca diagram venn unuk menentukan anggota himpunan | 16 |
| 17 | 4.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunan | Himpunan | 4.4.3. Menyebutkan himpunan bagian dari suatu himpunan | Menentukan pernyataan himpunan bagian | 17 |
| 18 | 4.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunan | Himpunan | 4.4.4. Menyatakan himpunan kuasa dari suatu himpunan | Menentukan anggota himpunan kuasa | 18 |
| 19 | 4.4 Menyelesaikan masalah kontekstual yang berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan kosong, komplemen himpunan | Himpunan | 4.4.6. Menyatakan irisan dari dua himpunan | Menentukan anggota irisan dari dua himpunan | 19 |
| 20 | 4.4
Menyelesaikan masalah kontekstual yang
berkaitan dengan himpunan, himpunan bagian, himpunan semesta , himpunan
kosong, komplemen himpunan |
Himpunan | 4.4.9. Menyelesaikan masalah kontekstual yang berkaitan dengan gabungan daridua himpunan | Menentukan anggota gabungan dari dua himpunan | 20 |
KISI-KISI PTS GANJIL KELAS VIII
B. 12, 17, 24 D. 11, 14, 17
B. 10, 7 D. 8, 5
3. Tentukan huruf yang hilang dari pola: A, B, D, ...,G, J, J, M, N.
A. E C. G
B. F D. H
4. Tiga pola selanjutnya dari 1, 3, 4, 7, 9, 11, 16, ..., ..., ....
A. 15, 25, 19 C. 20, 16, 28
B. 18, 23, 26 D. 20, 25, 26
5. Tiga pola selanjutnya dari 5, 4, 9, 8, 13, 12, 17, ..., ..., ....
A. 18, 23, 22 C. 16, 21, 20
B. 17, 22, 21 D. 15, 20, 19
6. Dua pola selanjutnya dari 1, 3, 4, 7, 9, 13, 16, 21, ..., ....
A. 27, 31 C. 25, 30
B. 25, 31 D. 25, 29
7. Perhatikan pola bilangan berikut.
(2, 6), (3, 11), (5, 19)
Pernyataan yang tepat untuk mendapatkan bilangan kedua dari bilangan pertama pada
A. ditambah 4
D. dikalikan 2 kemudian dikurangi 1
8. Titik-titik yang ada di kuadran III adalah ....
A. (6, 5) C. (6, -5)
B. (-6, 5) D. (-6, -5)
9. Koordinat titik A adalah (-5, 3). Jarak titik A dari sumbu-Y adalah ....
A. 5 satuan C. -3 satuan
B. 3 satuan D. -5 satuan
10. Koordinat titik berikut yang berjarak 7 satuan dari sumbu-X dan 4 satuan dari sumbu-Y adalah....
A. (7, 4) C. (4, 3)
B. (-7, 4) D. (-4, -7)
11. Garis k melalui (-3, 5) dan (0, 5). Sedangkan garis m melalui (-3, 3) dan (-1, 3). Posisi
B. sejajar sumbu Y D. berpotongan dgn sumbu X
A. (0, 3) C. (5, 4)
B. (4, 0) D. (4, 3)
A. trapesium C. argenjang
B. persegi panjang D. persegi
14. Diketahui titik A(0, 0), B(6, 0), dan D(2, 3). Maka koordinat titik C agar ABCD menjadi trapesium sama kaki adalah....
A. (3, 4) C. (0, 6)
B. (4, 3) D. (3, 2)
15. Diketahui A = {x | 1 ≤ x < 4, x ∊ A}, B = {2, 3, 5, 7}. Banyaknya fumgsi dari A ke B
A. 7 C. 64
B. 12 D. 81
16. Suatu fungsi f(x) = mx + n. Jika f(-2) = -9 dan f(3) = 11,
A. -4 dan 1 C. -4 dan -1
B. 4 dan 1 D. 4 dan -1
17. Suatu fumgsi dengan rumus f(x) = 4 - 2x², f(-5) adalah ....
A. -46 C. 46
B. 54 D. 104
18. Diketahui g : x → x² - 5x + 4 dengan domain {-2, -1, 0, 1, 2} maka daerah hasilnya
A. {-2. 0, 6, 10, 15} C. {-2, 0, 4, 10, 18}
B. {-2, 0, 4, 8, 10} D. {-2, 0, 6, 8, 18}
19. Jika f(x) = x² + 2 dan g(x) = 2x + 5 dan f(x) = g(x). maka x adalah ....
A. 3 atau 1 C. 3 atau -1
B. -3 atau 1 D. -3 atau -1
20. Himpunan berikut yang merupakan fungsi adalah ....
A. {(1, 1),(1, 2), (1, 3), (1, 4), (1, 5)}
B. {(1, 2),(2, 3), (3, 4), (4, 5), (5, 6)}
C. {(4, 2),(4, 3), (3, 1), (3, 2), (1, 1)}
D. {(4, 2),(3, 2), (2, 2), (2, 3), (1, 2)}
-
Senin, 10 Agustus 2020 Kelas : 7A & 7B Assalamualaikum Wr. Wb Selamat pagi Semua ! Apa Kabar Soleh/Soleha ? … Sem... -
POSISI GARIS TERHADAP SUMBU -X DAN SUMBU-Y KELAS : VIIIC HARI,TGL : Senin, 19 Agustus 2019 Dua garis sejajar adalah dua garis yan... -
Bunga Tunggal Hari/tgl : Kamis, 06 Februari 2020 Kelas : VII E & VII F Bunga tunggal adalah bunga uang yang diperoleh pada setiap akh...