Menghitung Perbandingan Sisi Sisi Pada Segitiga Siku-Siku
- Segitiga Siku – siku sama sisi ( segitiga sudut 45° )
Perhatikan gambar dibawah ini :
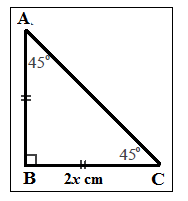
Segitiga ABC di atas merupakan segitiga siku – siku sama sisi , dengan sudut siku – siku di B dan ∠CAB= ∠BCA = 45° dan panjang BC = 2x . Dengan demikan , panjang BC = AB , dan BC = 2x . Lalu berapakah panjang AC ?
Untuk mecari panjang AC , maka kita masukkan pada rumus pythagoras sebagai berikut :
AC = √ BC2 + AB2
= √2x2 + 2x2
= √8x2
=2x √2
Maka dihasilkan , rumus sbb :
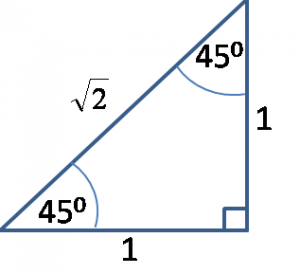
perbandingan sisi – sisi pada segitiga siku – siku sama sisi adalah tinggi : alas : sisi miring = 1 : 1 : √2
atau rumus cepat nya adalah :
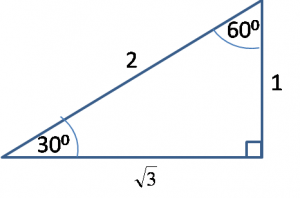
2. Segitiga siku – siku dengan sudut 30°, 90°, 60°
Perhatikan gambar di bawah ini :
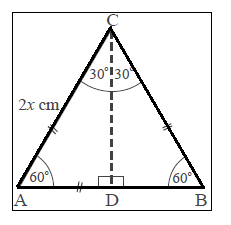
Segitiga ACB diatas merupakan segitiga sama sisi , dan apabila di potong menjadi dua menghasilkan dua segitiga siku – siku yaitu ∆ ADC , Siku – siku di D dan ∆ BDC , siku – siku di D juga . dan di hasilkan juga ∠CAD = ∠CBD =60° , ∠ACD = ∠BCD = 30° , ∠ADC = ∠BDC = 90° . Serta diketahui panjang AC = 2x . Kali ini , kita fokuskan pada ∆ ADC yang telah diketahui panjang AC = 2x , untuk mencari AD dan CD kita gunakan rumus pythagoras sebagai berikut :
CD = √ AC2 – AD2
= √ 2x2 – x2
= √ 4x2 – x2
= √ 3x2
CD = x √ 3
Maka di hasilkan rumus :
Jadi , perbandingan segitiga istimewa dengan sudut 30°, 90°, 60° adalah alas : tinggi : sisi miring = 1 : √3 : 2
atau rumus cepatnya adalah :
Contoh Soal :
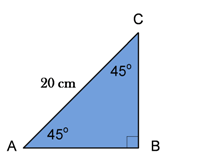
- Perhatikan gambar segitiga siku – siku dibawah ini :
Tentukan panjang AB , apabila diketahui panjang AC = 20 cm !
Penyelesaian :
Diketahui AC = 20cm ,
Ditanya AB = . . . .?
Jawab :
Gunakan Rumus :
maka AB = 1/2 a√2
= 1/2 . 20√2
AB = 10√2
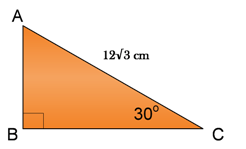
2. Perhatikan gambar di bawah ini :
Tentukan panjang CB dan AB , apabila diketahui panjang AC = 12√3 !
Penyelesaian :
Diketahui AC = 12√3
Ditanta CB dan AB = . . . ?
Jawab :
ingat rumus di bawah ini :
maka dihasilkan :
CB = 1/2 . a√3
= 1/2 . 12√3 .√3
= 1/2 .12 . 3
= 18 cm
AB = 1/2.a
=1/2 . 12√3
= 6√3 cm
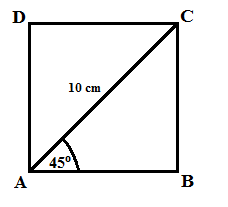
3. Perhatikan gambar di bawah ini :
Gambar di atas merupakan bangun persegi yang terbelah menjadi 2 segitiga , dengan panjang garis potong ( AC) =10cm , dan ∠CAB = 45°. Maka tentukan :
a. panjang AB
b. Luas persegi ABCD
c. Keliling persegi ABCD
Penyelesaian :
a. Panjang AB = . . .?
gunakan rumus :
AB = 1/2 . a√2
AB = 1/2 . 10√2
AB = 5√2
b. Luas persegi ABCD = s x s
= 5√2 x 5√2
= 50 cm2
c. Keliling Persegi ABCD = 4s
= 4 (5√2 )
= 20 √2
4. Sebuah ∆ ADC , dengan ∠DAC = 60°. dan panjang AC = 14cm . Tentukan panjang AD !
Penyelesaian :
masukan ke rumus :
di misalkan AC = a , AD = 1/2a√3
maka di hasilkan
AD = 1/2a√3
AD = 1/2 . 14√3
AD = 7√3 cm
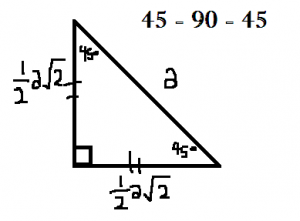
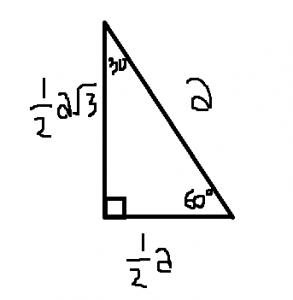

Tidak ada komentar:
Posting Komentar