Garis Singgung Persekutuan Luar Dua Lingkaran
Ulasan materi terkait garis singgung lingkaran yang pertama akan dibahas adalah garis singgung persekutuan luar dua lingkaran. Persamaan garis singgung lingkaran persekutuan luar melibatkan dua lingkaran dan sebuah garis singgung lingkaran. Untuk lebih jelasnya dapat dilihat pada gambar di bawah.
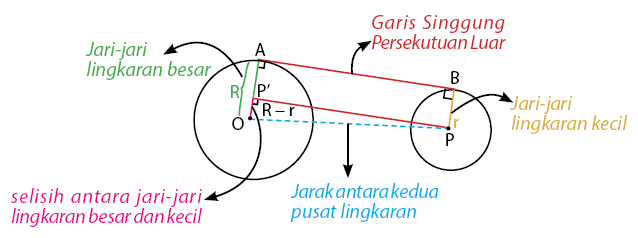
Garis AB adalah garis singgung persekutuan luar dua lingkaran. Konsep untuk mengetahui panjang garis singgung persekutuan luar dua lingkaran adalah teorema pythagoras. Langkah pertama adalah proyeksikan titik P ke garis OA. Panjang garis PP’ sama dengan garis AB, sehingga dengan menghitung panjang PP’ maka kita juga akan mendapatkan panjang AB (garis singgung persekutuan dua lingkaran).
Perhatikan bahwa segitiga PP’O merupakan segitiga siku-siku yang siku-siku di P’. Dengan teorema phytagoras dapat diperoleh panjang PP’ yaitu sebagai berikut.
![\[ PP' = \sqrt{OP^{2}-\left( OP'\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-0f6d507ed636becc2ad2fe97e815c860_l3.svg "Rendered by QuickLaTeX.com")
Karena 
maka,
![\[ PP' = \sqrt{OP^{2} - \left( R - r\right)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6f6807b7580568961ad1dbda5d5d0fa3_l3.svg "Rendered by QuickLaTeX.com")
Sehingga, rumus garis singgung persekutuan luar dua llingkaran dapat dinyatakan dalam rumus di bawah.
Rumus mencari panjang garis singgung persekutuan luar dua lingkaran:
![\[ AB = PP' = \sqrt{OP^{2}-(R-r)^{2}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e3287382bcab3661c25486ef3a1e5cea_l3.svg "Rendered by QuickLaTeX.com")
Keterangan:
AB = PP’ = Garis singgung persekutuan luar lingkaran
OP = Jarak antara kedua pusat lingkaran
R = Jari-jari lingkaran besar
r = jari-jari lingkaran kecil
Tidak ada komentar:
Posting Komentar