Faradiba: Hubungan Sudut Pusat dan Sudut Keliling

Hari/tgl : Rabu, 05 Februari 2020

Kelas : VIII A

Sudut Pusat

Sudut pusat adalah sudut terkecil yang dibentuk oleh pusat lingkaran dan dua titik yang terletak pada busur lingkaran. Gambar di bawah akan menunjukkan letak sudut pusat secara lebih jelas.

Sudut Pusat dan Sudut Keliling

Keterangan:
$\angle AOB$ merupakan sudut pusat yang menghadap busur AB.
$\angle COD$ merupakan sudut pusat yang menghadap busur CD.

Sudut Keliling

Sudut keliling adalah sudut yang dibentuk oleh tiga titik yang terletak pada busur lingkaran. Perhatikan gambar berikut untuk mengetahui letak sudut keliling dalam sebuah ligkaran.

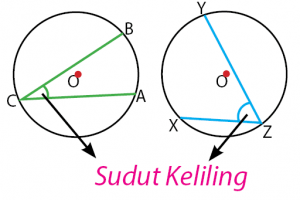
sudut pusat dan sudut keliling

Keterangan:
$\angle BCA$ merupakan sudut pusat yang menghadap busur AB.
$\angle XZY$ merupakan sudut pusat yang menghadap busur XY.

Hubungan Besar Sudut Pusat dan Sudut Keliling

Besar sudut pusat dan sudut keliling yag menghadap busur yang sama memiliki hubungan. Jadi, jika suatu besar sudut pusat diketahui, maka sudut keliling yang menghadap busur yang sama juga dapat diketahui. Hubungan antara sudut pusat dan sudut keliing dapat dinyatakan dalam uraian di bawah.

Perhatikan gambar di bawah!

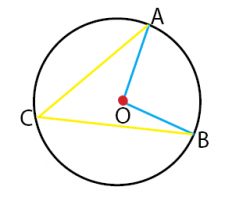
sudut pusat dan sudut keliling

Besar sudut pusat adalah dua kali besar sudut keliling yang menghadap busur yang sama.

$\angle AOB = 2 \times ACB$

Besar sudut keliling adalah setengah dari besar sudut pusat yang menghadap busur yang sama.

$\angle ACB = \frac{1}{2} \times AOB$

Besar sudut keliling yang menghadap busur yang sama adalah sama.
Untuk kasus ini, perhatikan gambar di bawah!

Perhatikan $\angle ACB$ , $\angle AXB$ , dan $\angle AYB$ ! Ketiganya menghadap busur yang sama, yaitu AB. Maka besar ketiga sudut tersebut adalah sama, $\angle ACB$ = $\angle AXB$ = $\angle AYB$ .

Jumlah dari sudut keliling yang saling berhadapan adalah $180^{o}$ .

Perhatikan gambar di bawah!

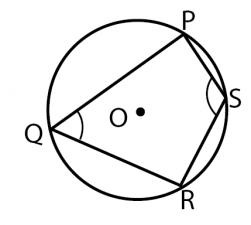
Hubungan antara dua sudut keliling $\angle PSR$ dan $\angle PQR$ adalah

$\angle PSR + \angle PQR = 180^{o}$

Contoh Soal dan Pembahasan

Contoh Soal Sudut Pusat dan Sudut Keliling
Perhatikan gambar berikut!

Jika besar sudut AOB adalah $40^{o}$ maka besar $\angle ACD$ adalah ….

Pembahasan:
Garis DB merupakan garis lurus (Ingat!!! Besar sudut pada garis lurus adalah 180 derajat

$\angle AOD + \angle AOB = 180^{o}$

$\angle AOD + 40^{o} = 180^{o}$

$\angle AOD = 180^{o} - 40^{o}$

$\angle AOD = 140^{o}$

Selanjutnya, perhatikan bahwa $\angle ACD$ dan $\angle AOD$ berturut-turut merupakan sudut pusat dan sudut keliling yang menghadap busur yang sama yaitu AD, sehingga